BAS3: A New Measure of Overall Athleticism

Burst, Agility, Strength and Speed in Standard Deviations

Author’s Note: This article talks about some of the theory and data behind the BAS3 measure of athleticism. I’ve tried to keep math and cumbersome statistical terms out of it as much as possible, but I’m afraid some was inevitable. It might facilitate reading if you first download the Excel spreadsheet and explore the calculations and instructions a bit.

Also, a quick special thanks for some early input from George Kritikos and Brian Malone at DLF, Telperion from the DLF Forum for his football data warehouse, TheFFGhost for his help with the final presentation of the data and Marty Jackson for help with some of the math and with figuring out the name.

And finally, I encourage anyone to use the BAS3 measure in their own research, or to modify it. I just ask that you please cite the author and the Dynasty League Football site when you do so.

The question of player athleticism is an important and controversial one. It seems obvious athleticism should somehow correlate with success in the NFL and both dynasty players and NFL teams themselves closely watch the NFL Combine and Pro Days. Uncovering the relationship between athleticism and success is difficult, because many other things also matter that aren’t accounted for and are difficult or impossible to measure. A relatively unathletic player may have excellent technique, a top-notch work ethic and high coachability that more than not offsets any physical limitations. Conversely, an athletic superstar may struggle with any or all of those things, or fall to nagging injuries or even find themselves lacking opportunity to show what they’re capable of because they’re buried behind an entrenched starter.

My goal here is not to dig into the question of how athleticism relates to performance, but to instead back up a step and think about how we measure athleticism.

SPARQ, Speed Score, and Others

There are a number of existing measures that attempt to summarize player athleticism into a single number, perhaps the most well-known of which is SPARQ. This was developed by NIKE for prep athletes on their way to college. Unfortunately, the formula for how they determine SPARQ scores is secret – we know what measures they use (height, weight, 40 yard dash, kneeling power ball throw, shuttle and vertical jump), but the end number emerges from a proverbial black box. A player’s measurements go in and a final number comes out.

There have been several attempts to reverse-engineer SPARQ scores based on the known inputs and apply them to players headed to the NFL, which do a fair job of approximating the final results. There are several problems with this, however:

1. We’re assuming this formula applies the same to high school athletes and college athletes.
2. We have to substitute bench press for kneeling power ball throw and we have to drop some measures we often have that NIKE doesn’t use (3 cone, broad jump). If possible, you never want to end up discarding relevant data when you already have it.
3. We’re assuming SPARQ is an optimal way to measure athleticism. Since we don’t know how SPARQ is calculated, this assumption is based almost entirely on whatever credibility it gains from the NIKE name. This underscores one of the main attributes of an “athleticism” measure – it’s not a real value we can measure directly. Rather, it’s one we have to infer from things we can measure by using good reasoning and methods.

A New Measure of Athleticism: BAS3

[am4show have=’g1;’ guest_error=’sub_message’ user_error=’sub_message’ ]

In developing a new measure of athleticism, I had two primary goals: One, create a logical, consistent and transparent measure that anyone can access, and two, create a measure that does not directly relate unit changes in dissimilar events. A good example of why this second goal matters is the common version of “Speed Score” (SS) that uses the equation: SS = 200*Weight / 40Time^4. I’ll spare you the math, but suffice to say that if you set the Speed Score to any constant value, this equation relates an entire range of values of 40Time to a corresponding value for Weight. Lower 40Time by one second, find out exactly how much Weight needs to go up to keep the same Speed Score.

That’s a very specific and highly dubious thing to propose without lots of supporting theory. Now, imagine making an assumption like this to relate all eight metrics we gain just from the NFL Combine. What’s the tradeoff between broad jump and bench press? Shuttle and height? All models involve some assumptions, but to avoid this particular mess of prickly assumption-making, the core of BAS3 revolves around using standard deviations from the mean.

Again sparing the math, a “standard deviation” is a way to measure how dispersed a set of data is, expressed in the units of measure themselves. That is to say, the standard deviation of all player’s 40-yard dash times is expressed in seconds, the standard deviation of bench press is measured in reps, and so on. Once the standard deviation for a given measure is calculated, you can simply find out how far an individual player is from the average, then divide that average by the standard deviation – the result is the number of standard deviations they are above or below the mean.

Note: At this point some of you may be recalling some statistics and thinking of the normal distribution (or “bell curve”). This is a type of distribution where each standard deviation corresponds to a percentage of the population, which tells us, for example, that about 95% of a population falls within two standard deviations of the mean. It’s possible all of the measures we are looking at here come from normal distributions, but that assumption will not be necessary to the result. In short, those corresponding percentages do not apply to these values.

By using standard deviations from the mean, we can compare dissimilar measures without needing to consider messy questions like how a bench press score relates to a 3-cone score. What we are comparing instead is how far a player is from average in each category, expressed in a standardized unit. So, a player who is zero standard deviations from the mean in both the 40-yard dash and bench press is exactly average in each metric, and THAT is something we can relate across events.

One fairly small side effect of this is that adding new players to our sample will very slightly change the scores for all players in the sample. So when we include data from the 2016 class, every player from 1999-2015 will be tweaked slightly. This results from the fact that averages and standard deviations are calculated based on the entire population’s values. Change those values, change the results. However, unless two players were extremely close to each other in the end score AND the incoming group of players differs strongly from the previous players, all ordinal rankings will remain the same.

For ease of interpretation, the final BAS3 figures are normalized so the least athletic player in the sample will always have a value of 0 and the most athletic will have a value of 100. They are also rounded out to one decimal point, even though it does make a few players look equal when they are really separated by a small amount. The necessary level of precision for this data to distinctly rank all players is 5 decimal points, which makes it cumbersome to read. Since the number of players affected is very small, it wasn’t much of a sacrifice to make in the name of readability.

The Inputs

In order to be relevant to as many players as possible, I restricted myself to only the inputs that are widely available, such as those officially reported by the Combine and commonly at Pro Days. This means measures such as arm length, hand size and the 10 and 20 yard dash times are discarded. As mentioned before, we never want to discard data if we can avoid it. In this case, however, including them resulted in dropping too many observations. It’s certainly possible (with better data) to work on including them in a future version of BAS3.

One other element I am not using is height. I find height to be implausible as a measure of athleticism. Imagine two hypothetical players:

Does the top player really seem more athletic? I find that hard to argue. Additionally, height can be a physical advantage or disadvantage. RBs tend to be shorter, WRs tend to be taller. But some receivers are short (Steve Smith Sr, 5’9”) and some running backs are tall (Adrian Peterson, 6’1”). I feel like height is better considered in addition to an athleticism score, not as part of it.

Weight, on the other hand, is used just like the other metrics. If you imagined those two players from above, but dropped height and made one of them weigh 180 pounds and the other 240 while keeping all other measures the same, I think it is fairly obvious that the same scores for the heavier player suggest a higher level of athleticism than they do for the lighter player. Take for example, JJ Watt (6’5”, 290 pounds) and Justin Hardy (5’10”, 192 pounds) who both had 4.21 Shuttle times. It strikes me as self-evident that Watt’s suggests far greater athleticism due to his extra 98 pounds.

One of the assumptions I make is that, broadly speaking, being truly elite in one category and average in all others is “more athletic” than being slightly above average in all categories. Or in a simple example, being four standard deviations above the mean in one category and exactly at the mean in the other six categories results in a higher end score than being one standard deviation above the mean in four categories and exactly at the mean in the remaining three. Mathematically, this is accomplished through squaring the figures. This strikes me as a good assumption for two reasons:

1. The specifics are subject to the exact distribution of the population, but it’s reasonable to assume that being two standard deviations from the mean is more than twice as hard as being one standard deviation from the mean.
2. A player who is truly elite in one category should have an opportunity to exploit that category to their advantage. That is, a player who is extremely fast can play the game in a way that lets them use that speed, thus giving them an advantage over a player who is merely above average at everything.

A problem arises from this emphasis on elite over above average, because two pairs of our measures are highly related – broad and vertical jump, and 3 cone and shuttle. The first two are measures of explosion and lower-body power, while the other two are measures of agility. If a player is particularly agile, then they likely have a very good value in both 3 cone and shuttle. If we square both of those values in our calculations, we’re essentially double-emphasizing the same measure. Therefore, I combine 3 cone and shuttle into a single “agility” score by averaging a player’s standard deviations from the mean in each. I do the same for broad and vertical jump into a “burst” category. This move is supported both by the descriptions of events on the NFL Combine website, and by plotting the categories against each other and looking at how related they are.

Rather than go through the rest of the calculations here, the exact steps (and some more detailed instructions) are available in the accompanying Excel spreadsheet.

Without Further Ado

If you’ve stuck with me this far, thank you! Now that I’ve kept you waiting through a glance into the muck (if you skipped through it all to the end, I forgive you), here’s a snapshot of the top 15 most athletic players of 2015 and 2014 according to BAS3. Note that my sample does not include lineman.

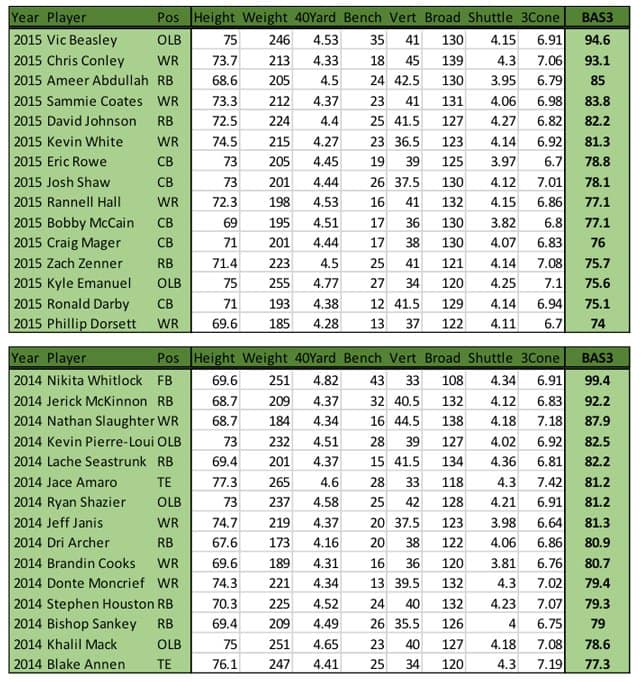
I’ll explore some of the data and its implications more in a future article, but a glance at this snapshot suggests it is quite in line with the general narrative about who is “athletic.”

Vic Beasley is an example of a player who is above average in every category, but enough so that he still beats out guys who are particularly elite in a smaller number of categories, such as Chris Conley. Beasley’s weakest category is his 40-yard dash, where he is still .41 standard deviations above the mean, while his strongest is Bench where he is almost 3. Conley, on the other hand, is actually below average in Weight, Bench and Shuttle and almost exactly average in 3 cone. However, he is 3.2 standard deviations above the mean in Vert and Broad, and 1.66 in 40Yard. Nikita Whitlock is an even more extreme example of a truly elite athlete in one category. His 43 Bench is an unheard-of 4.4 standard deviations above the mean, the highest value for any player in any category since 1999.

Of course, he’s also an example of how athleticism doesn’t directly translate to NFL success, as he was an undrafted free agent who has done short stints with at least three teams (mainly on practice squads) in the span of less than two years. Hopefully, with the help of BAS3, we can do more exploration into who succeeds and who doesn’t at the NFL level.

[/am4show]